Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- oracle
- map
- 생년
- 병합정렬
- 디자인패턴
- boot
- degien pattern
- 초(second)
- 자바
- 널체크
- ThreeWayPartition
- 분(minute)
- java
- 시(hour)
- 스트레티지패턴
- 자바스크립트
- Flyweight Pattern
- 파사드패턴
- JavaScript
- 매일프로그래밍
- 시간더하기
- SSL설정
- SpringBoot
- 알고리즘
- 곱 최대값
- list
- 조인
- json
- spring
- jQuery
Archives
- Today
- Total
만들어가는 세상
[JAVA] 최대값, 최소값 알고리즘 응용 문제 본문
문제를 풀어보진 않았습니다. 개념 이해 및 공유 차 내용 포스팅 합니다.
문제
정수 배열이 주어졌을 때, 배열 안에서 곱이 최대가 되는 두 정수를 찾으시오.
매일프로그래밍 문제 기준
Input: [-10, -3, 5, 6, -2]
Output: [-10, -3] 또는 [5, 6]풀이1
단순한 방법은 모든 쌍에 대해 곱을 계산하는 것입니다. 계산한 쌍의 곱이 이전보다 크면 새로운 쌍의 곱과 두 수를 저장하면서 가장 큰 곱을 찾아갑니다.
class FindMaximumProduct {
public static void findMaximumProduct(int[] A) {
int max_product = Integer.MIN_VALUE;
int max_i = -1, max_j = -1;
// 모든 원소들의 쌍을 계산
for (int i = 0; i < A.length - 1; i++) {
for (int j = i + 1; j < A.length; j++) {
// 두 수의 곱이 현재까지의 최대값보다 크면 최댓값 업데이트
if (max_product < A[i] * A[j]) {
max_product = A[i] * A[j];
max_i = i;
max_j = j;
}
}
}
System.out.print("Pair is (" + A[max_i] + ", " + A[max_j] + ")");
}
// 메인 함수
public static void main (String[] args) {
int[] A = { -10, -3, 5, 6, -2 };
findMaximumProduct(A);
}
} 시간 복잡도: O(n^2)
공간 복잡도: O(1)
결과
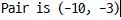
풀이2
배열을 정렬함으로써 시간 복잡도를 개선할 수 있습니다.정렬된 배열 내에서 곱이 가장 큰 두 정수는 배열 가장 앞의 두 수이거나 가장 끝의 두 수입니다.
import java.util.Arrays;
class FindMaximumProduct {
public static void findMaximumProduct(int[] A) {
// n은 배열의 길이
int n = A.length;
// 배열을 정렬
Arrays.sort(A);
// 두 수의 곱이 최대가 되는 경우는
// 가장 앞의 두 수의 곱이나 가장 끝의 두 수의 곱
if ((A[0] * A[1]) > (A[n - 1] * A[n - 2])) {
System.out.print("Pair is (" + A[0] + ',' + A[1] + ')');
} else {
System.out.print("Pair is (" + A[n - 1] + ',' + A[n - 2] + ')');
}
}
// 메인 함수
public static void main (String[] args) {
int[] A = { -10, -3, 5, 6, -20 };
findMaximumProduct(A);
}
}시간 복잡도: O(nlog(n))
공간 복잡도: O(1)
결과

풀이3
이 문제는 배열을 한 번 순회하면서 가장 큰 두 수와 가장 작은 두 수를 찾음으로써 선형시간에 풀 수 있습니다.
class FindMaximumProduct {
// 배열에서 곱이 최대가 되는 두 정수 찾는 함수
public static void findMaximumProduct(int[] A) {
// 가장 큰 두 수를 저장하는 변수
int max1 = A[0], max2 = Integer.MIN_VALUE;
// 가장 작은 두 수를 저장하는 변수
int min1 = A[0], min2 = Integer.MAX_VALUE;
for (int i = 1; i < A.length; i++) {
// 현재 원소가 최댓값보다 크면 가장 큰 두 수를 업데이트
if (A[i] > max1) {
max2 = max1;
max1 = A[i];
}
// 현재 원소가 두 번째 최댓값보다 크면 두 번째 최댓값 업데이트
else if (A[i] > max2) {
max2 = A[i];
}
// 현재 원소가 최솟값보다 크면 가장 작은 두 수를 업데이트
if (A[i] < min1) {
min2 = min1;
min1 = A[i];
}
// 현재 원소가 두 번째 최솟값보다 크면 두 번째 최솟값 업데이트
else if (A[i] < min2) {
min2 = A[i];
}
}
// 두 수의 곱이 최대가 되는 경우는
// 가장 큰 두 수의 곱이나 가장 작은 두 수의 곱
if (max1 * max2 > min1 * min2) {
System.out.print("Pair is (" + max1 + ", " + max2 + ")");
}
else {
System.out.print("Pair is (" + min1 + ", " + min2 + ")");
}
}
// 메인 함수
public static void main (String[] args) {
int arr[] = { -10, -3, 5, 6, -2 };
findMaximumProduct(arr);
}
}시간 복잡도: O(n)
공간 복잡도: O(1)
결과

'IT > JAVA' 카테고리의 다른 글
| [JAVA] 파사드 패턴 (facade pattern) 개념 (0) | 2020.04.17 |
|---|---|
| [JAVA] 병합 정렬 개념 및 알고리즘을 이용한 코딩#2 (0) | 2020.04.16 |
| [JAVA] 계수 정렬(Counting Sort) 개념 및 알고리즘을 이용한 코딩 (0) | 2020.04.14 |
| [JAVA] 병합 정렬 개념 및 알고리즘을 이용한 코딩#1 (0) | 2020.04.13 |
| [JAVA] 스트레티지 패턴 (strategy pattern) 개념 (0) | 2020.04.12 |
Comments




